Cooncan, by Robert Frederick Foster
SUGGESTIONS FOR GOOD PLAY
For Four or Five Players
There is probably no better way to illustrate the tactics of any game than that invented by “Cavendish” for the game of whist, which was to show the play of every card at the table from start to finish. One or two examples of this nature will probably give the reader a better grasp of the principles of the game than anything else.
If we call the players A B C D and E and suppose that B has the deal, A will be the first player on his left. Let us suppose that the stock card is the jack of hearts and that A holds these cards:










It is clear that the stock card does not connect with anything in the band, although it might be taken and held in the hope of getting the queen and so making a sequence of J Q K A, but it is usually better to take a chance on the pack when the stock card is of no positive value and is of large denomination, as these large cards are expensive things to be left with.
Let us suppose that A draws the 8 of clubs. He can now lay down a sequence of four clubs, or the 5 6 7 of clubs and three eights. Without endorsing such a procedure, but just to show how things turn out, let us suppose that he lays down these six cards, and look at the rest of his hand.
He has a chance on later rounds to fill out a sequence of 4 5 6 in hearts, if he can draw the 5, or three kings if he can catch a king of any denomination, or a sequence of A K Q, if he can draw a queen of hearts.
But these are not all equal chances, because there are more kings of all denominations than there are queens of hearts or fives of hearts. If he gets another king, the ace of hearts becomes useless. To discard either the 4 or 6 of hearts renders the other worthless, so the best discard is the heart ace, which is placed on the stock, face upward, covering the jack of hearts.
This leaves A with 30 points in his hand to pay for in case the game comes to an end before it gets round to him again; two kings at 10 each, a 4 and a 6. The moment A discards, it is B’s turn to play, because the discard once made it cannot be changed, nor can the player lay down any more cards.
B has the choice of drawing the ace of hearts from the stock or taking a card from the top of the pack, but he cannot touch the jack of hearts, which is covered, and will never be in play again unless the pack runs out before any one wins the game. Even if the ace of hearts is drawn and used, the discard that takes its place will cover the jack of hearts.
B and those following him, have the advantage that they can not only get rid of combinations of their own, but they may add to the combinations laid out by A. This is called fattening. Let us suppose the second player, B, holds these cards:










The ace of hearts is of no use to this hand and is an expensive card to keep, so B draws from the pack and gets the 5 of hearts. This card is of no use to him, unless he calls the joker a 5 and lays down three, but that would break up the diamond sequence and the joker may be used to much better advantage. He might call it the 6 or 9 of spades and lay down the 7 and 8 with it. Then he could lay down three fours and discard the spade king, leaving himself with four disconnected cards.
Another plan would be to call the joker a 6 and lay down three of them and three fours, but a better way would be to call the joker the 4 of diamonds and lay down the 6 5 joker in diamonds and three fours, discarding the king of spades and hoping for the spades to connect up.
The reader should observe that it would be a mistake to call the joker the 7 of diamonds, because one 8 of diamonds is already exposed on the table and there is only one card in the pack that would carry the sequence any further in that direction. But by calling the joker the 4, there are two chances to get the 3 of diamonds, and if the 8 comes the joker can be shifted to the place of the 7.
Should the other 8 of diamonds turn up, it would almost certainly be added to the three eights already on the table by whoever drew it. B could add his 8 of spades to these three eights, but as he can do that at any time, it is better to hold it on the chance of getting the spade 6 or 9. which will get rid of the spade 7. The best discard is the spade king, because it is of no use, and counts more than the heart 5, another useless card.
This leaves B with 26 paints to pay for in case the game ends before it gets round to him again. He has a sequence of 5 6 7 8 in his hand, but as they are not of the same suit, he cannot lay them down. The reader must remember that his laying down at all is not endorsed, but is simply used to illustrate what may happen.
The third player, C, will now have four layouts which he may fatten, besides any combinations of his own. Let us suppose he holds these cards, the spade king on the stock:










By taking the spade king from the stock, be can lay down three kings and three fives, but the rest of his hand is apparently dead-wood, as he needs the 10 or 7 of diamonds to complete that sequence, and the 5 or 7 of spades to connect that one. This would leave him only one discard, the spade 4, and two sequences to fill.
But instead of this discouraging outlook, C has the game won, as he can get rid of every card in his hand at once, thanks to the combinations laid out by A and B.
To begin with, he lays out the three kings and three fives. Then he adds the 8 of spades to the three eights already on the table and the 4 of spades to the three fours. His next move is to shift the joker from its position as the 4 of diamonds to the other end, calling it the 7 and making it connect with his 8 and 9 in that suit. Finally he discards the spade 6 and wins the game, being all down. This is a good illustration of a “splash.”
This example is given to impress upon the reader the disadvantage of laying down combinations too early in the play. After one or two players have made up their hands pretty well and begin to lay down cards seven or eight at a time, it is expedient to get rid of as much as you can, as some one is liable to go game at any moment.
The more combinations there are on the table, the greaser the number of opportunities offered to players to get rid of their odd cards by fattening. If the combinations are held up until all or nearly all the cards can be laid down at once, no other player can lay anything but complete combinations of his own, upon which you may get rid of your odd cards. Of course this holding up is at the risk of some player’s having picked up cards that fill his hand and being able to lay them all down, and then the players who have been holding up will have to pay for all their cards.
In the example hand just given, we can see that the only cards C would have been able to lay down from his own hand were three kings and three fives, which would have left him with four odd cards, worth 31 points. Instead of this he is able to get rid of these 31 points, the exposed joker being particularly useful to him.
Here is an example of a different style of game:
Let us suppose that the stock is the queen of clubs and that the first player, A, holds these cards:










If A takes the club queen from the stack, he can use it in two ways: It will make a sequence with the ace and king of clubs, or part of three queens. If the ace of clubs is taken in as part of a sequence, the deuce of clubs becomes of no value and may be discarded, If the deuce is held, in the hope of drawing the 3, than the king of clubs is of no value and may be discarded.
Holding cards in the hope of getting others to connect with them is bad policy in this game unless the chance is is in favor of those cards on account of the number of them in the pack. If you have two kings, there are eight cards in the pack that will make you a triplet, six kings and two jokers. If you have the 2 and 4 of hearts, there are only four cards that will fill; two treys and two jokers. If any joker has been shown, or any trey of hearts is on the table, say in a triplet, your chances are so much the less. This teaches us always to keep in mind the fact that the chances of filling any combination depend on the number of cards still to show that will fit, and among the cards that have shown one must not for- get those covered up in the stock.
One important point to remember is, that it is always easier to fill a triplet than a sequence when playing with the double pack, even if the sequence is an open-end. If you hold the 7 and 8 of hearts, there are only six cards in the pack that will enable you to lay down a sequence. These are two sixes, two nines and two jokers. If only one card will fit, such as when you hold A K or A 2, the chances of filling it are still more remote, not only because there are only two cards and two Jokers that will fit, but because these end cards are almost invariably laid out in triplets by other players, diminishing your chance of getting them.
When there is a choice of discards, it is always better to hold the cards that may fill in either way, cards that are good for sequence or triplet. In A’s cards, for instance, the club 2 will fit into a sequence with the ace if a trey turns up, but both the spade queens will have to be held until a fourth queen appears if the queen of clubs is used in sequence with the ace and king.
Now comes the question of probability. There are only four treys of clubs in the pack, counting jokers, but there are seven more queens, counting jokers, and also seven more treys of all suits. It is therefore much easier to get another queen to lay down a triplet with the spade queens than it is to get a trey of clubs to fit the ace and deuce, a further objection to the sequence being that it is not open at both ends.
Turning our attention to the diamonds, there are two queens, two nines and two jokers, any of which will fit the J 10. That gives us 6 chances as against 4 to get the trey of clubs, so that the proper discard from this hand is the deuce of clubs.
But before discarding, the player must make up his mind whether or not he will lay out any of his combinations, because after he discards it is too late.
It is always a disadvantage to lay out too much for the others to fatten, and the first player should always be willing to take a chance that the draw goes round once, if not oftener, before any player can lay down ten cards, and that will give him another opportunity to fill in. It is when the cards held show that it is clearly impossible to get everything down in less than two or three rounds, that the player should cut down his losses as early and as surely as possible.
With A’s cards, it is clearly impossible to get everything down in less than two more rounds, and they would have to be lucky ones to hit the exact cards wanted, because of the discard, which is an important thing to provide for, If A gets another queen next time, be will have to break up the diamonds, and then he must get a fourth queen, or a trey, or the jack of clubs, to get rid of the other diamond. This is supposing that he holds the A K Q of clubs and three treys, discarding the club deuce.
That A will have any such luck is highly improbable and he cannot hope to survive for four rounds, so his policy should be to shed as much of his expensive holdings as he can or he may have to pay for them. If he lays out the three high clubs and the three treys, he gets rid of 40 points at once. This not only saves so much if he has to settle, but may open the way to induce others to lay out and give A a chance to fatten with his odd cards. Normally, A’s chance to win is nil.
As this game gets better known and results are more closely observed, we shall probably arrive at a correct estimate of the average duration of a hand in rounds, which will enable us to judge more closely the probability of a given hand, requiring a known number of draws to fill it, surviving long enough to win.
If A lays out the A K Q of clubs and three trays, discarding the deuce of clubs, it is B’s turn. Let us suppose he holds these cards:










The stock being of no use to him, he draws from the pack and gets the king of diamonds, This gives him two kings, two queens, two nines, and two fours, but nothing to lay out. As none of the odd cards connect with anything, it is better to lay out the one that would cost the most if it had to be paid for, so he discards the diamond 7.
The next player, C, holds these cards, with the 7 of diamonds on the stock:










By taking the stock, C can lay down every card in his hand but one. He has no sequence, but can lay down three sevens and three tens. He can fatten A’s club sequence with the jack and add to the three treys. He could lay the joker anywhere and call it anything, and after discarding he would have only the heart 5 or the spade 4 left in his hand.
But if the joker is laid down, its position is in a measure fixed, and it is usually better to hold it, in the hope of making either a sequence or a triplet with the card that is kept with it, even at the risk of having to pay 15 points for the joker if some other player wins the game. If you hold any named card and the joker, say the 10 of clubs, there are no less than sixteen cards in the pack that will lay them both down. These are the other joker, seven tens, and the eight eights, nines, jacks and queens of clubs.
When we come to C’s discard, after he has laid down eight cards, it is better to lay down the spade, although it counts a point less than the heart, because the chance of improvement in spades is less, two treys of spades being on the table, whereas nothing has been passed or laid out in connection with the 5 of hearts.
The next player, D, holds these cards, the spade 4 on the stock:










When a player has laid down eight of his cards it is time to run, and as the 4 of spades is of no use to D, he draws from the stock and gets the 6 of hearts. This gives him an interesting problem. In the first place, he can fatten the treys on the table with the 3 of clubs and lay out three sixes and three kings. He still has 4o points left, 10 of which he can discard, but which combinations shall he keep? The 10 of hearts on the table might suggest keeping the diamond, but either is a guess.
It is only when we look ahead to the discard that we see the neccessity of changing our views as to the cards that should be laid down in sequence or triplets. Instead of guessing which of two suits to keep for a sequence, it is better to keep a chance for a triplet, and the proper layout for D is the sequence of K Q J in hearts, three sixes, and the 3 of clubs, keeping the two kings, and a diamond which can be discarded if a third king comes along.
It now comes to the dealer, E, with the queen of diamonds on the stock and these cards:










The diamond queen is of no use to E and is an expensive card to hold, so he draws and gets the 6 of spades. In view of the danger from C, who has but two cards left, E should get down all he can, and he is fortunate in being able to get rid of every card hut one.
His ace of hearts goes to the head of the heart sequence on the table. He adds his two black sixes to these already shown by D. Then he calls the joker the 7 of diamonds and lays down the sequence, 5 6 7 8 9. His discard will he the jack of hearts, keeping the 9, but where will he place the 10 of clubs?
This brings us to a point in laying down that many players are careless about. If the club 10 is put on the sequence, it opens the way for some other player to got rid of the 9; but if it is put with the tens, any player with the club 9 is still barred out, whereas nothing could stop a player with another 10, as the combination is already on the table for him to fatten. For this reason E should place his 10 with the others, but for the purpose of illustration we shall suppose he adds it to the club sequence, discarding the heart jack and keeping the 9, as no nines have been shown yet.
Apropos of the play of this club 10, a player will sometimes have a sequence of three that he can either lay down himself or add to a sequence already on the table. As a rule it is better to join the two than to lay them out separately.
Suppose the A K Q of clubs have been shown, and you hold the J 10 9. If you lay yours down apart, you leave three openings for other players to fatten, and four cards available, not counting jokers. Two eights and a queen will fit on yours, and a jack will fit the other. By joining the sequences, you shut out the queen and jack, and leave an opening for nothing but the eights.
We now get round to the first player, A, who still holds his two spade queens and the J 10 of diamonds, with the heart jack on the stock. This is too expensive a card to take at this stage of the game, so he draws from the pack and gets the club 7. He adds this to the seven on the table, puts his 10 with the others, discards the jacks of diamonds and has to keep his two queens and hope for another chance to get a third, which will allow him to lay them down without a discard.
It now comes to B, who laid down nothing. He draws a card and gets the heart 10. This connects his 9 to the sequence on the table, and he adds the 4 of diamonds to the diamond sequence and the club 9 to that sequence. As no 3 of hearts has been shown, there is still hope that he may get one to make a sequence of 2 3 4, and he has a chance for three kings or three queens, although the hope of another draw is slight, he must risk it and discard the spade 5.
This card puts C game, as he takes it, lays down his own 5 of hearts and calls the joker a third 5.
A has to pay for two queens, 20 points. B has to pay for six cards, 46 points. D has to pay for three cards, 30 points. E has to pay for the heart 9, 9 points.
So that C wins a total of, 105 points.
If more than one game is played without settling, the scores may be kept by ruling a pad in double columns for each player’s plus and minus, or the ordinary bridge washbook will answer the purpose. Taking the foregoing results for the first game, and let us suppose that on the second A is the winner, B and C losing 54 each; D 28, and E 11. The washbook would have this appearance:
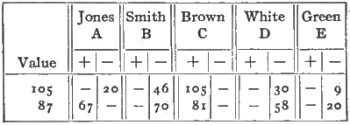
As a check, the total points won ahoul,I be recorded in the left hand margin. To prove the score, see that the total losses on each line equal the total winnings. In the foregoing, A and C are 67 and 81 plus, 148; while B D and E are 70, 58 and 20 minus, 148, so the score balances.
This is a portion of a full-text reproduction of Robert Frederick Foster's book "Cooncan (Conquián): A Game of Cards Also Called Rum", which was published in 1913, by Frederick A. Stokes Company, and is now in the public domain. The text of the book was OCR'd from a vintage copy of the book, and is provided as an educational resource for Rummy players, researchers, and students of the game. Any grammatical or typographical errors are an artifact of this process, and should not be attributed to the author.
Cooncan, by Robert Frederick Foster - Table of Contents
